16日目「とうとう来たよ、つるかめ算が」

中学受験をしなければ経験しない単元っていうのがいくつかあります。

中学受験未経験なわたしにとって、そのレベルの高さに驚かされるばかりですが、中には全くやったことのない問題もあります。

その代表と言えるのが「つるかめ算」です。

中学受験に挑む子たちにとって、避けて通れない、しかし重要単元であるこの問題。かえで（長男）と一緒にわたしも「つるかめ算」に挑むのでした。

本当につるとかめなのね。

つるとかめが合わせて10匹います。足の数の合計が24本であるとき、かめは何匹いますか。

日能研のテキストより

上記は「つるかめ算」の基本的な問題です。本当につるとかめが出てくるから「つるかめ算」っていうんですね。

つるは足が2本、かめは足が4本、足の数の差異を用いて答えを求める計算方法ですね。別につるとかめでなくても良かったと思うけど、「鶴は千年、亀は万年」っていう故事成語からきているのでしょうか。

基本レベルはいける。ちょっと説明したらかえでも分かったみたいで、そのあとは一人で解けるようになりました。

面積図・・・だと？

さて、間口は広く、されどそれは深淵の入り口に過ぎなかった・・・というのが算数ですよね。「つるかめ算」もご多分に漏れず、ちょっと踏み込むと難易度が一気にアップします。

こういちさんは、A地点から3200ｍのところにあるＢ地点まで、自転車で行きました。初めは分速180mで進んでいましたが、途中のＣ地点から分速250ｍにスピードアップして進んだところ、出発してから17分後に着きました。

Ｃ地点を通過したのは、出発してから何分後でしたか。

日能研のテキストより

これくらいのレベルになると、「面積図」というものを書いて考えるのがよいとのこと。和差算のときは横軸だけの「線分図」だったけど、早くも縦軸が加わりましたよ。さらに「分速」っていうワードも出ていますので、分速180ｍなら1分間で180ｍ進む速さだよ～という説明も要ります。

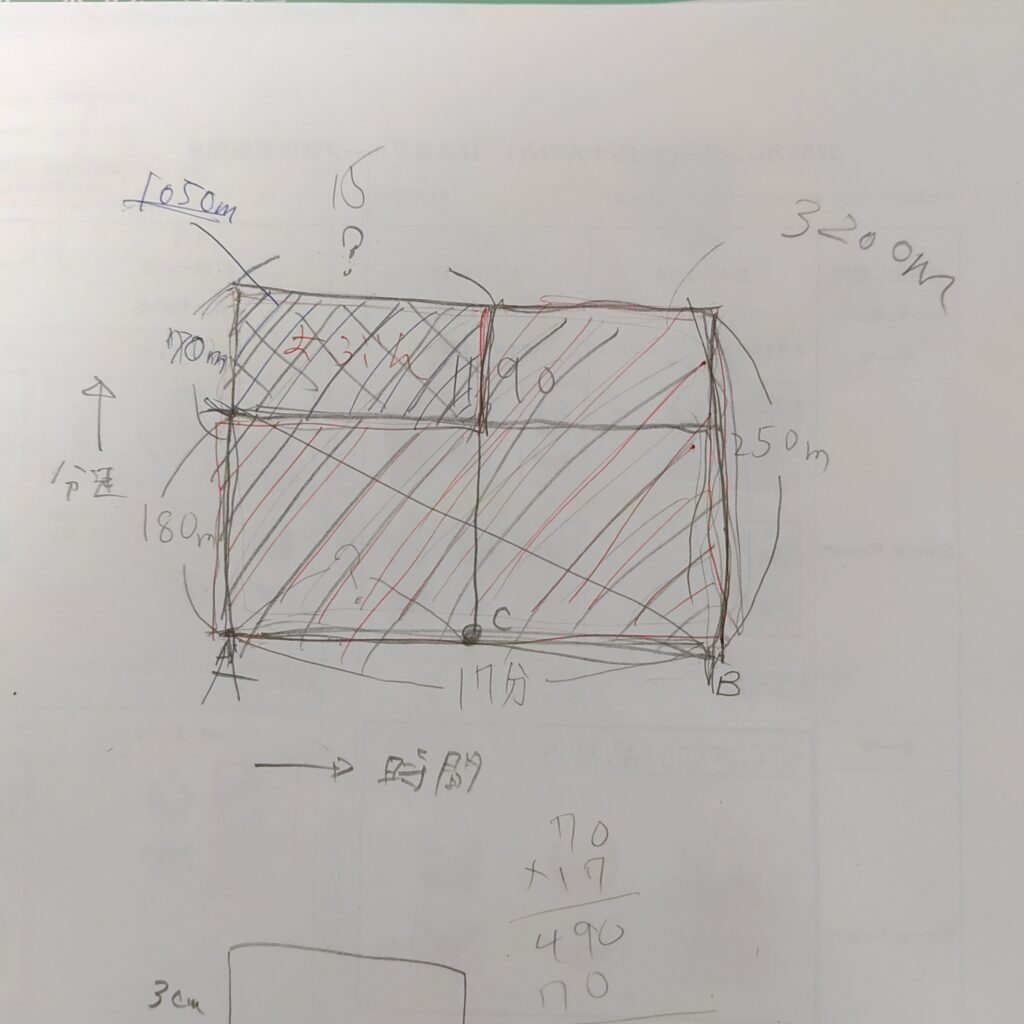
かえでと悪戦苦闘した面積図がこれです。

赤の面積が3200ｍ（実際に進んだ距離）だから、17分間を分速250ｍで進んだ場合（4250ｍ）から、赤の面積を差し引くと青の面積が1050ｍってわかるよね。分速250ｍと180ｍの速さの差は70ｍだから、1050÷70で横軸（分）が分かるよね～と教えました。

困ったときはYouTubeで解説動画を見るようにしているのですが、何度か聞くと「面積図」で求められる原理が分かりますね。正直、これが小学生レベルなのかって感じですけど(;^ω^)

数式じゃなくて図式をおこさないといけない。図形問題にも強くないとなかなか難しいですね。